Uma abordagem bayesiana para a previsão de séries temporais
Hoje, vamos implementar uma regressão linear bayesiana em R a partir do zero e usá-la para prever o crescimento do PIB dos EUA. Este post é baseado em um manual muito informativo do Banco da Inglaterra sobre a Econometria Bayesiana Aplicada . Traduzi o código original do Matlab para o R desde a sua fonte aberta e amplamente utilizado em análise de dados / ciência. Meu principal objetivo neste post é tentar dar às pessoas uma melhor compreensão das estatísticas bayesianas, algumas de suas vantagens e também alguns cenários em que você pode querer usá-las.
Vamos tirar um momento para pensar sobre o porquê de querermos usar as técnicas Bayesianas em primeiro lugar. Bem, há algumas vantagens em fazê-lo e estas são particularmente atraentes para a análise de séries temporais. Um problema ao trabalhar com modelos de séries temporais é o ajuste excessivo, particularmente ao estimar modelos com grande número de parâmetros em períodos de tempo relativamente curtos. Este não é um problema neste caso particular, mas certamente pode ser quando se olha para múltiplas variáveis, o que é bastante comum na previsão econômica. Uma solução para o problema do ajuste excessivo é adotar uma abordagem bayesiana que nos permita impor certas prioridades em nossas variáveis.
Para entender por que isso funciona, considere o caso de uma Regressão de Ridge (penalidade L2). Esta é uma técnica de regularização que nos ajuda a reduzir o encaixe (boa explicação da regressão de rebentamento) penalizando-nos quando os valores dos parâmetros aumentam. Se, em vez disso, adotássemos uma abordagem bayesiana do problema de regressão e usássemos um prior normal, estaríamos basicamente fazendo exatamente a mesma coisa que uma regressão de rebordo. Aqui está um vídeo passando pela derivação para provar que eles são os mesmos (realmente bom curso BTW). Outro grande motivo que muitas vezes preferimos usar métodos Bayesianos é que nos permite incorporar a incerteza em nossas estimativas de parâmetros, o que é particularmente útil na previsão.
Teoria Bayesiana
Antes de irmos direto a ela, vamos discutir algumas noções básicas da teoria Bayesiana e como ela se aplica à regressão. Normalmente, se alguém quisesse estimar uma regressão linear do formulário:


Eles começariam coletando os dados apropriados em cada variável e formariam a função de verossimilhança abaixo. Eles então tentariam encontrar o B e o σ² que maximizam essa função:

Neste caso, os parâmetros ótimos podem ser encontrados tomando a derivada do log desta função e encontrando os valores de B onde a derivada é igual a zero. Se realmente fizéssemos as contas, encontraríamos a solução como sendo o estimador OLS abaixo. Eu não vou entrar na derivação, mas aqui está um vídeo muito legal derivando as estimativas do OLS em detalhes. Podemos também pensar neste estimador como a covariância de X e Y dividida pela variância de X.
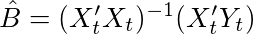
O valor ideal da variância seria igual a

onde T é o número de linhas no nosso conjunto de dados. A principal diferença entre a abordagem freqüentista clássica e a abordagem bayesiana é que os parâmetros do modelo são baseados exclusivamente nas informações contidas nos dados, enquanto a abordagem bayesiana nos permite incorporar outras informações através do uso de um prior . A tabela abaixo resume as principais diferenças entre as abordagens frequentista e bayesiana.
Então, como usamos essa informação prévia? Bem, isso é quando Bayes Ruleentra em jogo. Lembre-se que a fórmula da regra de Bayes é:
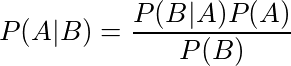
Aqui está uma explicação muito clara e um exemplo da regra de Bayes sendo usada. Ele demonstra como podemos combinar nosso conhecimento prévio com evidências para formar uma probabilidade posterior usando um exemplo médico.
Agora vamos aplicar a regra de Bayes ao nosso problema de regressão e ver o que obtemos. Abaixo está a distribuição posterior dos nossos parâmetros. Lembre-se, isso é basicamente o que queremos calcular.

Podemos também dar um passo adiante e descrever a distribuição posterior de uma maneira mais sucinta.

Esta equação afirma que a distribuição posterior de nossos parâmetros condicionais aos nossos dados é proporcional à nossa função de verossimilhança (que assumimos ser normal) multiplicada pela distribuição prévia de nossos coeficientes (que também é normal). A densidade marginal ou F (Y) no denominador (equivalente a P (B) na regra de Bayes) é uma constante de normalização para garantir que nossa distribuição se integre a 1. Observe também que ela não depende de nossos parâmetros para que possamos omitir isto.
Para calcular a distribuição posterior, precisamos isolar a parte dessa distribuição posterior relacionada a cada coeficiente. Isso envolve o cálculo de distribuições marginais, o que na prática é extremamente difícil de fazer analiticamente. É aqui que um método numérico conhecido como amostragem de Gibbs é útil. O amostrador de Gibbs é um exemplo de Markov Chain Monte Carlo (MCMC) e nos permite usar desenhos da distribuição condicional para aproximar a distribuição marginal conjunta. O próximo passo é uma rápida visão geral de como isso funciona.
Amostragem de Gibbs
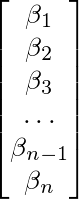
Imagine que temos uma distribuição conjunta de N variáveis:

e queremos encontrar a distribuição marginal de cada variável. Se a forma dessas variáveis for desconhecida, no entanto, pode ser muito difícil calcular as integrações necessárias analiticamente (a integração é difícil! ). Em casos como esses, seguimos os seguintes passos para implementar o algoritmo de Gibbs. Primeiro, precisamos inicializar valores iniciais para nossas variáveis,

Em seguida, mostramos nossa primeira variável condicional aos valores atuais das outras variáveis N-1. ou seja

Então, experimentamos nossa segunda variável condicional em todas as outras

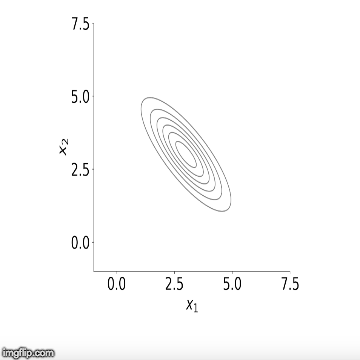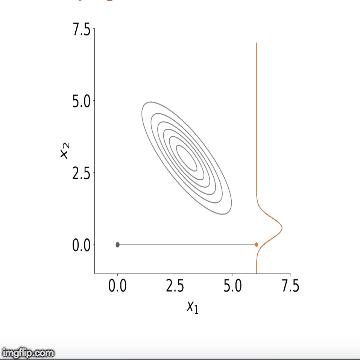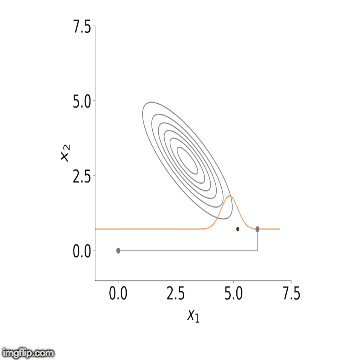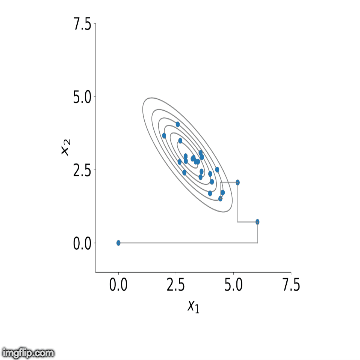
, repetindo isso até que tenhamos amostrado cada variável. Isso termina uma iteração do algoritmo de amostragem de Gibbs. À medida que repetimos esses passos, um grande número de vezes as amostras das distribuições condicionais convergem para as distribuições marginais conjuntas. Uma vez que tenhamos M corridas do amostrador de Gibbs, a média dos nossos sorteios retidos pode ser pensada como uma aproximação da média da distribuição posterior. Abaixo está uma visualização do amostrador em ação para duas variáveis. Você pode ver como inicialmente o algoritmo começa a amostragem a partir de pontos fora de nossa distribuição, mas começa a convergir para ele depois de várias etapas.
Agora que temos a teoria fora do caminho, vamos ver como isso funciona na prática. Abaixo está o código para implementar uma regressão linear usando o amostrador de Gibbs. Em particular, vou estimar um modelo AR (2) sobre o crescimento ano após ano no Produto Interno Bruto (PIB) trimestral dos EUA. Eu então usarei este modelo para prever o crescimento do PIB usando uma estrutura bayesiana. Usando essa abordagem, podemos construir intervalos confiáveis em torno de nossas previsões usando quantis da densidade posterior, ou seja, quantis dos desenhos retidos de nosso algoritmo.
Modelo
Nosso modelo terá a seguinte forma:

Também podemos escrever isso em forma de matriz definindo as seguintes matrizes.

B acima do qual é apenas um vetor de coeficientes e nossa matriz de dados X abaixo.

Isso nos dá a forma na equação 1 acima. Como eu já disse, nosso objetivo aqui é aproximar a distribuição posterior de nossos coeficientes:

e podemos fazer isso calculando as distribuições condicionais dentro de uma estrutura de amostragem de Gibbs. Tudo bem, agora que a teoria está fora do caminho, vamos começar a codificar isso em R.
Código
A primeira coisa que precisamos fazer é carregar os dados. Eu baixei o crescimento do PIB dos EUA no site do Federal Reserve of St. Louis ( FRED ). Eu escolho p = 2 como o número de atrasos que eu quero usar. Essa escolha é bem arbitrária e existem testes formais, como o AIC e o BIC, que podemos usar para escolher o melhor número de atrasos, mas eu não os usei para essa análise. Qual é o velho ditado? Faça o que eu digo não como eu faço. Eu acho que isso se aplica aqui. 😄
biblioteca (ggplot)
Y.df <- read.csv ('USGDP.csv', cabeçalho = TRUE) nomes <- c ('Data', 'GDP') Y <- data.frame (Y.df [, 2])
p = 2 T1 = nevoeiro (Y)
Em seguida, definimos a função regression_matrix para criar nossa matriz X contendo nossa variável GDP defasada e um termo constante. A função leva em três parâmetros, os dados, o número de lags e TRUE ou FALSE dependendo se queremos uma constante ou não. Eu também criei uma outra função auxiliar abaixo disso, que transforma a matriz de coeficiente de nosso modelo em uma matriz de formulário complementar. Esta função, ar_companion_matrix essencialmente transforma uma matriz de coeficientes como a abaixo (Observe que o termo constante não está incluído):
Em uma matriz n * n com os coeficientes ao longo da linha superior e uma matriz identidade (n-1) * (n-1) abaixo disso. Expressar nossa matriz dessa maneira nos permite calcular a estabilidade do nosso modelo mais tarde, que será uma parte importante do nosso Gibbers Sampler. Eu falarei mais sobre isso mais adiante no post quando chegarmos ao código relevante.
regression_matrix <- function (dados, p, constante) { nrow <- as.numeric (dim (dados) [1]) nvar <- as.numeric (dim (dados) [2]) Y1 <- as.matrix (dados , ncol = nvar) X <- embed (Y1, p + 1) X <- X [, (nvar + 1): ncol (X)] se (constante == TRUE) { X <-cbind (rep (1, (nrow-p)), X) } Y = matriz (Y1 [(p + 1): nrow (Y1),]) nvar2 = ncol (X) retorno = lista (Y = Y, X = X, nvar2 = nvar2 nrow = nrow }}
################################################## ##############
ar_companion_matrix <- function (beta) {
#check if beta é uma matriz if (is.matrix (beta) == FALSE) { stop ('erro: beta precisa ser uma matriz') } # não inclui constante k = nrow (beta) - 1 FF < - matriz (0, nrow = k, ncol = k) #segre identidade matriz FF [2: k, 1: (k-1)] <- diag (1, nrow = k-1, ncol = k-1) temp <- t (beta [2: (k + 1), 1: 1])
#Insira os coeficientes ao longo da linha superior
FF [1: 1,1: k] <- temp
return (FF)
}
Nosso próximo bit de código implementa nossa função regression_matrix e extrai as matrizes e o número de linhas da nossa lista de resultados. Também montamos nossas prioridades para a análise bayesiana.
resultados = list () resultados <- regression_matrix (Y, p, TRUE)
X <- resultados $ X Y <- resultados $ Y nrow <- resultados $ nrow nvar <- resultados $ nvar
# Inicializa Priores B <- c (rep (0, nvar)) B <- como.matriz (B, nevo = 1, ncol = nvar) sigma0 <- diag (1, nvar)
T0 = 1 # graus anteriores de liberdade D0 = 0,1 # escala anterior (teta0)
# valor inicial da variância sigma2 = 1
O que temos feito aqui é essencialmente um pré-requisito normal para nossos coeficientes Beta, que têm média = 0 e variância = 1. Para nossa média, temos prévias:
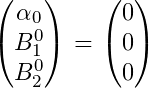
E para nossa variância nós temos priors:
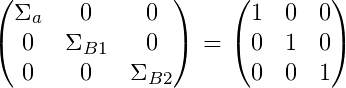
Para o parâmetro de variância , definimos uma gama inversa antes (conjugado antes). Essa é uma distribuição padrão a ser usada para a variância, pois é definida apenas para números positivos, o que é ideal para variação, pois ela só pode ser positiva.
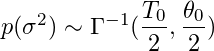
Para este exemplo, escolhemos arbitrariamente T0 = 1 e theta0 = 0.1 (D0 é o nosso código). Se quiséssemos testar essas opções de prioridades, poderíamos fazer testes de robustez, alterando nossas priori iniciais e verificando se alterava o posterior significativamente. Se tentarmos visualizar o que muda o valor de theta0, veríamos que um valor mais alto nos daria uma distribuição mais ampla, com nosso coeficiente mais propenso a assumir valores maiores em termos absolutos, semelhante a ter uma grande variação anterior em nossa versão Beta. .
repetições = 15000 queima = 4000 horizon = 14 out = matriz (0, nrow = reps, ncol = nvar + 1) nomes de col (out) <- c ('constante', 'beta1', 'beta2', 'sigma') out1 <- matriz (0, nrow = reps, ncol = horizonte)
Acima, definimos nosso horizonte de previsão e inicializamos algumas matrizes para armazenar nossos resultados. Nós criamos uma matriz chamado para fora que irá armazenar todos os nossos empates. Ele precisará ter linhas iguais ao número de empates de nosso amostrador, que nesse caso é igual a 15.000. Também precisamos criar uma matriz que armazene os resultados de nossas previsões. Como estamos calculando nossas previsões iterando uma equação do formulário:

Vamos precisar dos nossos últimos dois períodos observáveis para calcular a previsão. Isso significa que nossa segunda matriz out1 terá colunas iguais ao número de períodos de previsão mais o número de lags, 14 neste caso.
Implementação da Amostragem de Gibbs
OK, então o que se segue é um pedaço grande e complicado de código, mas eu irei passo a passo e espero que fique mais claro depois.
gibbs_sampler <- função (X, Y, B0, sigma0, sigma2, teta0, D0, reps, out, out1) {
# Main Loop for (i em 1: reps) {
if (i %% 1000 == 0) { print (sprintf ("Interação:% d", i)) }
# Média e Variância Posterior Condicional
M = resolver (resolver (sigma0) + como.umérico (1 / sigma2) * t (X)% *% X)% *%
(resolver (sigma0)% *% B0 + as.umérico ( 1 / sigma2) * t (X)% *% Y)
V = resolver (resolver (sigma0) + como.umérico (1 / sigma2) * t (X)% *% X)
chck = -1
while (chck <0 ) { # checar estabilidade
B <- M + t (rnorm (p + 1)% *% chol (V))
# Checagem: não estacionária por 3 lags
b = ar_companion_matrix (B)
ee <- máx (sapply (eigen) b) $ valores, abs))
se (ee <= 1) {
chck = 1
}
}
# computar residuais resids <- Y - X% *% B T2 = T0 + T1 D1 = D0 + t (resids)% *% resides [i,] <- t (matriz (c (t (B), sigma2) )) # extrair de Gama Inversa z0 = rnorm (T1.1) z0z0 = t (z0)% *% z0 sigma2 = D1 / z0z0 out [i,] <- t (matriz (c (t (B), sigma2) )) # computa previsões de 2 anos yhat = rep (0, horizonte) end = as.numeric (length (Y)) yhat [1: 2] = Y [(end-1): end,] cfactor = sqrt (sigma2) X_mat = c (1, rep (0, p))
para (m em (p + 1): horizonte) { para (atraso em 1: p) { # cria a matriz X com p lags X_mat [(lag + 1)] = yhat [m-lag] } #Use a matriz X em previsão de que [m] = X_mat% *% B + rnorm (1) * cfactor }
out1 [i,] <- yhat
} # fim do retorno de Gibbs Sampler = list (out, out1)
} results1 <- gibbs_sampler (X, Y, B0, sigma0, sigma2, T0, D0, reps, out, out1)
# burn first 4000 coef <- results1 [[1]] [(queima + 1): repetições,] previsões <- results1 [[2]] [(burn + 1): reps,]
Primeiro de tudo, precisamos dos seguintes argumentos para nossa função. Nossa variável inicial, neste caso, crescimento do PIB (Y). Nossa matriz X, que é apenas Y, é defasada em 2 períodos com uma coluna de anexos. Também precisamos de todas as nossas prioridades que definimos anteriormente, o número de vezes para iterar nosso algoritmo (reps) e, finalmente, nossas duas matrizes de saída.
O loop principal é o que precisamos prestar mais atenção aqui. É aqui que todos os principais cálculos ocorrem. As duas primeiras equações M e Vdescrevem a média e a variância posterior da distribuição normal condicional em B e σ². Eu não os deduzirei aqui, mas se você estiver interessado, eles estarão disponíveis em Análise de Séries Temporais por Hamilton (1994) ou em Reconhecimento de Padrões de Bispo e Capítulo 3 de Aprendizado de Máquina (embora com notação ligeiramente diferente). Para ser explícito, a média do nosso parâmetro posterior Beta é definida como:
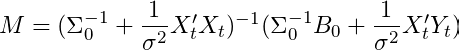
e a variância do nosso parâmetro posterior Beta é definida como:
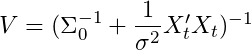
Se brincarmos um pouco com o segundo termo em M, podemos substituir nosso estimador de máxima verossimilhança por Y_t. Fazendo isso nos dá

Essencialmente, esta equação diz que M é apenas uma média ponderada de nossa média anterior e nosso estimador de máxima verossimilhança para Beta. Eu acho que intuitivamente isso faz muito sentido, já que estamos tentando combinar nossas informações prévias, bem como as evidências de nossos dados. Vamos considerar nossa variância anterior por um momento para tentar melhorar nossa interpretação dessa equação. Se atribuímos uma pequena variância prévia (sigma0), essencialmente, estamos confiantes em nossa escolha de antes e pensamos que nosso posterior estará próximo a ele. Neste caso, a distribuição será bastante apertada. Por outro lado, o oposto é verdadeiro se definirmos uma alta variação em nosso parâmetro Beta. Nesse cenário, o parâmetro Beta OLS será mais pesado.
Ainda não terminamos. Ainda precisamos obter um sorteio aleatório da distribuição correta, mas podemos fazer isso usando um truque simples. Para obter uma variável aleatória a partir de uma distribuição Normal com média M e variância V, podemos amostrar um vetor a partir de uma distribuição normal padrão e transformá-lo usando a equação abaixo.

Essencialmente, adicionamos nossa média e escala posterior condicional pela raiz quadrada de nossa variância posterior (desvio padrão). Isso nos dá nossa amostra B de nossa distribuição posterior condicional. O próximo bit de código também tem uma verificação para garantir que a matriz do coeficiente esteja estável, ou seja, nossa variável é estacionária, garantindo que nosso modelo seja dinamicamente estável. Ao redefinir nosso AR (2) como um AR (1) (formulário complementar), podemos verificar se os valores absolutos dos autovalores são menores que 1 (somente é necessário verificar se o maior autovalor é <| 1 |) . Se eles são, então isso significa que nosso modelo é dinamicamente estável. Se alguém quiser abordar isso com mais detalhes, recomendo o capítulo 17 dos Métodos Fundamentais de Economia Matemática ou apenas leia este post para uma introdução rápida.
Agora que temos nosso empate de B, extraímos sigma da distribuição de gama inversa condicional em B. Para amostrar uma variável aleatória da distribuição Gamma inversa com graus de liberdade

e escala

podemos amostrar variáveis T de uma distribuição normal padrão z0 ~ N (0,1) e então fazer o seguinte ajuste

z é agora um empate da distribuição de gama inversa correta.
O código abaixo armazena nossos desenhos dos coeficientes em nossa matriz out. Em seguida, usamos esses desenhos para criar nossas previsões. O código essencialmente cria uma matriz chamada yhat, para armazenar nossas previsões para 12 períodos no futuro (3 anos desde que estamos usando dados trimestrais). Nossa equação para uma previsão de um passo à frente pode ser escrita como
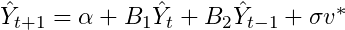
Em geral, precisaremos de uma matriz de tamanho n + p onde n é o número de períodos que desejamos prever e p é o número de defasagens usadas no AR. A previsão é apenas um modelo AR (2) com um choque aleatório a cada período que é baseado em nossos desenhos de sigma. OK, isso é muito bom para o código do amostrador da Gibbs.
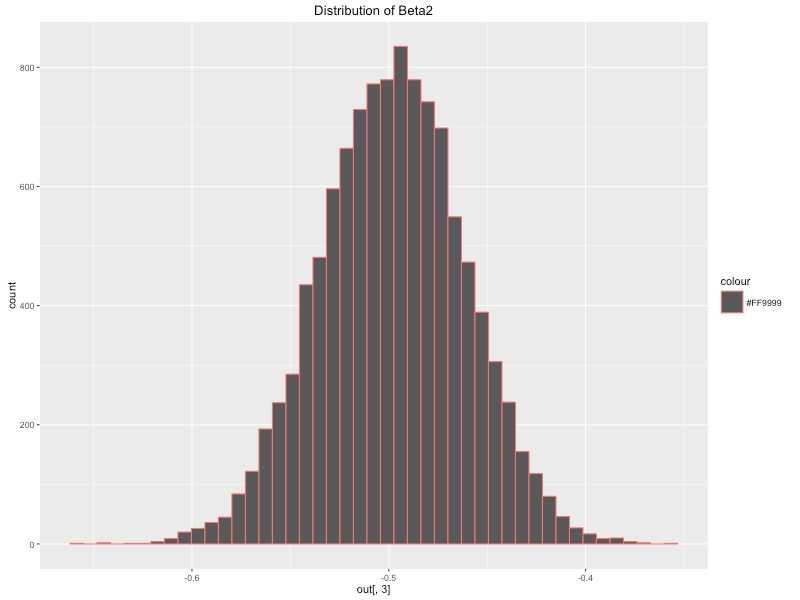
Agora podemos começar a ver o que o algoritmo produziu. O código abaixo extrai os coeficientes que precisamos que correspondem às colunas da matriz coef. Cada linha nos dá o valor do nosso parâmetro para cada sorteio do amostrador de Gibbs. Calcular a média de cada uma dessas variáveis nos dá uma aproximação da média posterior da distribuição para cada coeficiente . Essa distribuição pode ser bastante útil para outras técnicas estatísticas, como o teste de hipóteses, e é outra vantagem de se adotar uma abordagem Bayesiana à modelagem. Abaixo eu plotei a distribuição posterior dos coeficientes usando ggplot2. Podemos ver que eles se assemelham a uma distribuição normal, o que faz sentido, uma vez que definimos uma função normal de previsão e probabilidade. Os meios posteriores dos nossos parâmetros são os seguintes:
constante <- média (coef [, 1]) beta1 <- média (coef [, 2]) beta2 <- média (coef [, 3]) sigma <- média (coef [, 4])
qplot (coef [, 1], geom = "histograma", compartimentos = 45, principal = 'Distribuição de Constante', cor = "#FF9999") qplot (coef [, 2], geom = "histograma", compartimentos = 45 , main = 'Distribuição de Beta1', cor = "# FF9999") qplot (coef [, 3], geom = "histograma", compartimentos = 45, principal = 'Distribuição de Beta2', cor = "# FF9999") qplot (coef [, 4], geom = "histograma", compartimentos = 45, principal = 'Distribuição de Sigma', cor = "# FF9999")
A próxima coisa que vamos fazer é usar esses parâmetros para traçar nossas previsões e construir nossos intervalos confiáveis em torno dessas previsões.
Plotar nossas previsões
Abaixo está uma previsão de 3 anos para o crescimento ano a ano do PIB. Observe que o uso da análise bayesiana nos permitiu criar uma previsão com intervalos confiáveis, o que é muito útil para destacar a incerteza de nossas previsões. Observe que isso é diferente de um intervalo de confiança e é interpretado como um pouco diferente. Se estivéssemos adotando uma abordagem frequentista e executássemos um experimento 100 vezes, por exemplo, esperaríamos que nosso verdadeiro valor de parâmetro estivesse nesse intervalo em 95 dos 100 experimentos. Em contraste, a abordagem bayesiana é interpretada como o valor verdadeiro do parâmetro contido dentro dessa faixa com 95% de probabilidade. Essa diferença é sutil, mas muito importante.
biblioteca (matrixStats); biblioteca (ggplot2); biblioteca (reshape2)
#antigos para todos os pontos de dados, facilita a plotagem post_means <- colMeans (coef) forecasts_m <- as.matrix (colMeans (forecasts))
#Criando faixas de erro / intervalos credíveis em torno de nossas previsões error_bands <- colQuantiles (previsões, prob = c (0.16,0.84)) Y_temp = cbind (Y, Y)
error_bands <- rbind (Y_temp, error_bands [3: dim (error_bands) [1],]) todos <- as.matrix (c (Y [1: (comprimento (Y) -2)], forecasts_m))
forecasts.mat <- cbind.data.frame (error_bands [, 1], todos, error_bands [, 2]) nomes (forecasts.mat) <- c ('inferior', 'média', 'superior')
# criar vetor de data para plotar Data <- seq (as.Date ('1948/07/01'), por = 'quarter', length.out = dim (forecasts.mat) [1])
data.plot <- cbind.data.frame (Data, forecasts.mat) data_subset <- data.plot [214: 292,] data_fore <- data.plot [280: 292,]
ggplot (data_subset, aes (x = Data, y = média)) + geom_line (cor = 'azul', lwd = 1.2) + geom_ribbon (dados = data_fore, aes (ymin = inferior, ymax = superior, cor = "bandas" alfa = 0,2))
O código acima calcula os percentis 16 e 84 de nossas previsões para usar como intervalos confiáveis. Combinamos essas colunas com nossas previsões e plotamos um subconjunto dos dados usando ggplot e geom_ribbon para plotar os intervalos em torno da previsão. O enredo acima parece razoavelmente bom, mas eu gostaria de fazer isso um pouco mais bonito.
Eu encontrei um muito útil do blog post que cria gráficos de fãs muito semelhantes aos relatórios de inflação do Banco da Inglaterra. A biblioteca que eu uso é chamada de fanplot e permite plotar diferentes percentis de nossa distribuição de previsão, que parece um pouco melhor do que o gráfico anterior.
biblioteca (fanplot) forecasts_mean <- as.matrix (colMeans (out2)) forecast_sd <- como.matrix (aplicar (out2,2, sd)) tt <- seq (2018,25, 2021, por = 0,25) y0 <- 2018,25 params <- cbind (tt, forecast_mean [-c (1,2)], forecast_sd [-c (1,2)]) p <- seq (0,10, 0,90, 0,05)
# Calcular Percentis k = nrow (params) gdp <- matriz (NA, nrow = comprimento (p), ncol = k) para (i em 1: k) gdp [, i] <- qsplitnorm (p, modo = params [ i, 2], sd = params [i, 3])
# Traçar dados anteriores Y_ts <- ts (subconjunto dos dados $ média, frequência = 4, início = c (2001,1)) gráfico (Y_ts, tipo = "l", col = "tomate", lwd = 2.5, xlim = c ( y0 - 17, y0 + 3), ylim = c ( -4,6 ), xaxt = "n", yaxt = "n", ylab = "")
# background e fanchart rect (y0-0.25, par ("usr") [3] - 1, y0 + 3, par ("usr") [4], border = "gray90", col = "gray90") ventilador ( data = gdp, data.type = "valores", probs = p, inicio = y0, frequência = 4, âncora = Y_ts [tempo (Y_ts) == y0-.25], fan.col = colorRampPalette (c ("tomate "," gray90 ")), ln = NULL, rlab = NULL)
# BOE eixo estético (2, at = -2: 5, las = 2, tcl = 0.5, rótulos = FALSO) eixo (4, at = -2: 5, las = 2, tcl = 0.5) eixo (1, em = 2000: 2021, tcl = 0,5) eixo (1, at = seq (2000, 2021, 0,25), etiquetas = FALSO, tcl = 0,2) abline (h = 0) abline (v = y0 + 1,75, lty = 2) Linha de 2 anos
Conclusão
Nossa previsão parece bastante positiva, com uma previsão média de crescimento anual em torno de 3% até 2021. Também parece haver um risco positivo, com o intervalo de 95% de credibilidade subindo para quase 5%. O gráfico indica que é altamente improvável que haverá um crescimento negativo durante o período que é bastante interessante e, a julgar pelas políticas econômicas expansionistas nos EUA neste momento, isso pode se mostrar correto. As faixas de confiança são muito grandes, como você pode ver, indicando que há uma ampla distribuição no valor que o crescimento do PIB poderia ter sobre o período de previsão. Existem muitos outros tipos de modelos que poderíamos ter usado e, provavelmente, obter uma previsão mais precisa, como modelos bayesianos VAR ou modelos dinâmicos, que usam várias outras variáveis econômicas. Embora potencialmente mais preciso, esses modelos são muito mais complexos e muito mais difíceis de codificar. Para os propósitos de uma introdução à Regressão Bayesiana e para obter uma compreensão intuitiva dessa abordagem, um modelo AR é perfeitamente razoável.
Eu acho que é importante dizer por que eu escolhi fazer este tipo de modelo do zero quando há claramente maneiras muito mais fáceis e menos dolorosas de fazer este tipo de previsão. Eu tenho a tendência de achar que a melhor maneira absoluta de eu aprender algo complexo como esse é tentar reproduzir o algoritmo do zero. Isso realmente reforça o que eu aprendi teoricamente e me força a colocá-lo em um ambiente aplicado, o que pode ser extremamente difícil se eu não entendi completamente o assunto. Eu também acho que essa abordagem faz as coisas ficarem na minha cabeça um pouco mais. Na prática, eu provavelmente não usaria esse código, pois é provável que ele quebre com bastante facilidade e seja difícil de depurar (como já descobri), mas acho que essa é uma maneira muito eficaz de aprender.
OK pessoal, isso conclui este post. Espero que todos tenham gostado e aprendido um pouco sobre as Estatísticas Bayesianas e como podemos usá-las na prática. Se você tiver alguma dúvida, sinta-se à vontade para postar abaixo ou se conectar comigo via LinkedIn.












Comentários
Postar um comentário