Álgebra Linear explicada no contexto da aprendizagem profunda
Neste artigo, usei o método de cima para baixo para explicar a álgebra linear para aprendizado profundo. Primeiro, fornecendo os aplicativos e os usos e, em seguida, detalhando para fornecer os conceitos.
Definição de álgebra linear na wikipedia:
Álgebra Linear é o ramo da matemática referente a equações lineares e funções lineares e suas representações através de matrizes e espaços vetoriais.
Índice:
- Introdução.
- Perspectiva matemática de vetores e matrizes.
- Tipos de matrizes.
- Decomposição de matrizes.
- Normas
- Vectorização.
- Radiodifusão.
- Fontes externas.
Introdução:
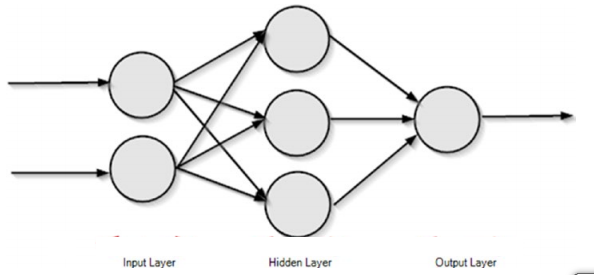
Se você começar a aprender profundamente, a primeira coisa a que será exposto é a rede neural feed forward, que é a rede mais simples e também muito útil em aprendizado profundo. Sob o capô, a rede neural feed forward é apenas uma função composta, que multiplica algumas matrizes e vetores juntos.
Não é que os vetores e as matrizes sejam a única maneira de fazer essas operações, mas eles se tornam altamente eficientes se você fizer isso.
A imagem acima mostra uma simples rede neural de feed forward que propaga a informação para frente.
A imagem é uma bela representação da rede neural, mas como um computador pode entender isso. Em um computador, as camadas da rede neural são representadas como vetores. Considere a camada de entrada como X e a camada oculta como H. A camada de saída não está preocupada por enquanto (o processo de computação de redes neurais de feed forward não está relacionado aqui).
Então, pode ser representado como vetores e matrizes como,
A imagem acima mostra as operações necessárias para calcular a saída para a primeira e a única camada oculta da rede neural acima (a computação para a camada de saída não é mostrada). Vamos acabar com isso.
Cada coluna da rede são vetores.Vectores são matrizes dinâmicas que são uma coleção de dados (ou recursos) .Na rede neural atual, o vetor ' x ' mantém a entrada.Não é obrigatório representar entradas como vetores, mas se você faz isso, eles se tornam cada vez mais convenientes para realizar operações em paralelo .
Aprendizagem profunda e em redes neurais específicas são computacionalmente caras, então elas exigem esse truque legal para fazê-las computar mais rápido.
Isso se chama vetorização. Eles tornam os cálculos extremamente mais rápidos.Esta é uma das principais razões pelas quais as GPUs são necessárias para o aprendizado profundo , pois elas são especializadas em operações vetorizadas como a multiplicação de matrizes (veremos isso no final em profundidade).
A saída da camada oculta H é calculada executando H = f ( W .x + b).
Aqui W é chamado de matriz de peso, b é chamado de preconceito e f é a função de ativação (este artigo não explica sobre redes neurais de feed forward, se você precisar de um primer sobre o conceito de FFNN, veja aqui .)
Vamos analisar a equação
o primeiro componente é W . x ; este é um produto vetor-matriz, porque W é uma matriz e x é um vetor. Antes de começar a multiplicá-los, vamos ter alguma idéia sobre as notações: geralmente vetores são denotados por pequenas letras em negrito e itálico (como x ) e matrizes são denotadas por letras maiúsculas em negrito e itálico (como X ). Se a letra é maiúscula e em negrito, mas não em itálico, então é um tensor (como X ).
Em uma perspectiva da ciência da computação:
Escalar: um único número.
Vector: Uma lista de valores (rank 1 tensor)
Matriz: Uma lista bidimensional de valores (rank 2 tensor)
Tensor: Uma matriz multidimensional com classificação n.
Perfurando abaixo:
Em uma perspectiva matemática:
Vetor:
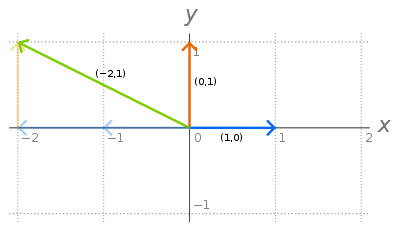
Um vetor é uma grandeza que tem magnitude e direção. É uma entidade que existe no espaço , sua existência é denotada por x ², se for um vetor bidimensional que existe no espaço real (cada elemento denota uma coordenada ao longo de um eixo diferente.)
Todos os vectores no espaço 2D pode ser obtido por combinação linear dos dois vectores chamados vectores de base . (Indicado por i e j) (De um modo geral, um vector em N dimensões pode ser representado por vectores de base N). Eles são unitários vectores normal, porque sua magnitude é uma e são perpendiculares entre si . Um desses dois vetores não pode ser representado pelo outro vetor. Então eles são chamados como vetores linearmente independentes . (Se algum vetor não puder ser obtido por uma combinação linear de um conjunto de vetores, então o vetor é linearmente independente daquele conjunto). Todo o conjunto de pontos no espaço 2D que pode ser obtido pela combinação linear desses dois vetores é dito ser o spanSe um vetor é representado por uma combinação linear (adição, multiplicação) do conjunto de outros vetores, então ele é linearmente dependente desse conjunto de vetores (não adianta adicionar este novo vetor ao conjunto existente. )
Quaisquer dois vetores podem ser adicionados juntos. Eles podem ser multiplicados juntos. Sua multiplicação é de dois tipos, produto de ponto e produto cruzado. Consulte aqui
Matriz:
Uma matriz é um array 2D de números. Eles representam transformações . Cada coluna de uma matriz 2 * 2 denota cada um dos 2 vetores base após o espaço 2D ser aplicado com essa transformação. Sua representação espacial é W ∈ ℝ³ * ² com 3 linhas e 2 colunas.
Um produto de vetor de matriz é chamado transformação desse vetor, enquanto um produto de matriz de matriz é chamado como composição de transformações.
Há apenas uma matriz que não faz nenhuma transformação para o vetor. É a matriz de identidade ( I ). As colunas de eu represento os vetores de base.
Determinante da matriz A, denotada por det ( A ), o fator de escala da transformação linear descrita pela matriz.
Por que uma perspectiva matemática é importante para pesquisadores de aprendizagem profunda? Porque eles nos ajudam a entender os conceitos básicos de design dos objetos fundamentais. Eles também ajudam na criação de soluções criativas para problemas profundos de aprendizado. Mas não se preocupe, existem muitos idiomas e pacotes que fazem essas implementações para nós. Mas também é bom saber suas implementações.
Uma dessas bibliotecas é insensível para a linguagem de programação python.
Há lotes de recursos para aprender numpy. (O que é muito importante para a aprendizagem de aprendizagem profunda, se você usar python.) Olha aqui .
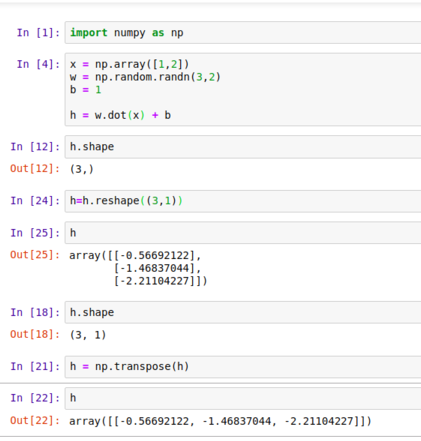
Aqui, o np.array cria um array numpy.
O np.random é um pacote que contém métodos para geração de números aleatórios.
o método dot é calcular o produto entre a matriz.
Podemos alterar a forma do array numpy e também verificá-lo.
aqui você pode ver que o produto de Wx é um vetor e é adicionado com b, que é um escalar. Isso expande automaticamente b como transpose ([1,1]). Essa cópia implícita de b para vários locais é chamada de difusão. (vamos ver em profundidade daqui a pouco)
Você observou a palavra transpor: A transposição de uma matriz é uma imagem espelhada da matriz através da linha diagonal (da parte superior esquerda para a parte inferior direita da matriz).
## numpy code para transpor import numpy como np A = np.array ([[1,2], [3,4], [5,6]]) B = np.transpose (A) ## ou B = AT
Tipos de matrizes:
Matriz diagonal : Todos os elementos são zero, exceto os elementos diagonais principais.
Matriz de identidade : uma matriz diagonal com valores diagonais como 1.
## numpy code para criar a importação de matriz de identidade numpy como np a = np.eye (4)
Matriz simétrica : uma matriz que é igual à sua transposição. A = transpor (A)
Matriz singular : uma matriz cujo determinante é zero e as colunas são linearmente dependentes. Sua classificação é menor que o número de linhas ou colunas da matriz.
Decomposição de matrizes:
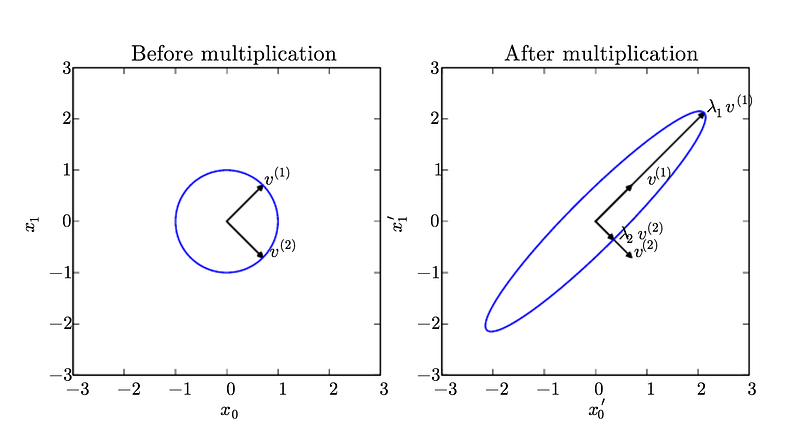
uma decomposição de matriz ou fatorização de matriz é uma fatoração de uma matriz em um produto de matrizes. Existem muitas decomposições matriciais diferentes; cada um encontra uso entre uma classe particular de problemas. Um dos tipos mais amplamente usados de decomposição de matriz é chamado de decomposição eigen , na qual nós decompomos uma matriz em um conjunto de autovetores e autovalores.
Um vetor Eigen de uma matriz quadrada A é um vetor não zero v tal que a multiplicação por A altera somente a escala de v.
UMA . v = lambda. v
aqui v é o vetor eigen e lambda é o valor eigen.
## numpy programa para encontrar vetores eigen. de numpy import array de numpy.linalg import eig # define matriz A = array ([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print (A) # calcula a composição de eigend valores, vetores = eig (A) print (valores) print (vectors)
A decomposição Eigen é muito útil no aprendizado de máquina. É particularmente útil para conceitos como redução de dimensionalidade.
Para mais sobre eigen decomposição, consulte o livro de aprendizagem profunda, capítulo 2
Existem também várias outras técnicas de decomposição de matrizes usadas em aprendizado profundo. Olhe aqui.
Normas:
Overfitting e underfitting:
W hen você assistir a uma palestra aprendizagem profunda, muitas vezes você ouvir o overfitting prazo e termos underfitting.These descrever o estado da precisão do modelo de aprendizagem profunda.
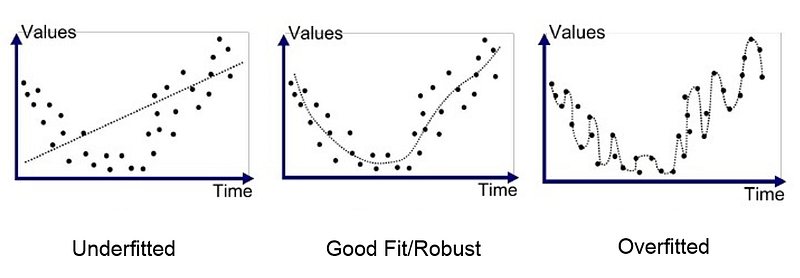
Overfitting refere-se a um modelo que aprende os dados de treinamento muito bem.Ele literalmente assaltou os dados de treinamento.Nos modelos de overfit, a precisão do treinamento é muito alta e a precisão da validação é muito baixa.
Os modelos de underfit não conseguiram aprender os dados de treinamento. Nos modelos underfit, a precisão do treinamento e validação são ambos muito baixos.
O overfitting e o underfitting podem levar a um fraco desempenho do modelo. Mas, de longe, o problema mais comum no aprendizado de máquina aplicado é o superajuste.
Para reduzir o overfitting, temos que usar uma técnica chamada Regularização. Evita que os dados de treinamento sejam assaltados, para evitar o risco de overfitting.
É a responsabilidade mais importante do engenheiro de aprendizagem profunda criar um modelo que se adapte geralmente à entrada. Existem vários métodos de regularização. Mais notavelmente a regularização L1 (Lasso) e a regularização L2 (Ridge).
Os detalhes destes não são fornecidos, mas para entender estes você deve saber o que é uma norma.
Norma:
A norma é o tamanho do vetor. A fórmula geral para a norma de um vetor x é dada por,
a norma L² com p = 2 é chamada de norma euclidiana, porque é a distância euclidiana entre origem e x.
A norma L is é simplesmente a soma de todos os elementos do vetor. Ela é usada no aprendizado de máquina quando o sistema requer muito mais precisão. Para diferenciar claramente entre um elemento zero e um elemento diferente de zero. A norma L¹ é também conhecida como norma de Manhattan .
Existe também a norma max, que é o valor absoluto do elemento de maior magnitude.
O equivalente da norma L² para uma matriz é a norma frobenius.
Não apenas na regularização, as normas são usadas também em procedimentos de otimização.
Ok, agora, depois de todos esses conceitos e teorias, chegamos para cobrir a parte mais importante necessária para o aprendizado profundo. Eles são vetorização e transmissão.
Vectorização:
É o truque de reduzir a execução de loops e executar o processo em paralelo, fornecendo dados como vetores.
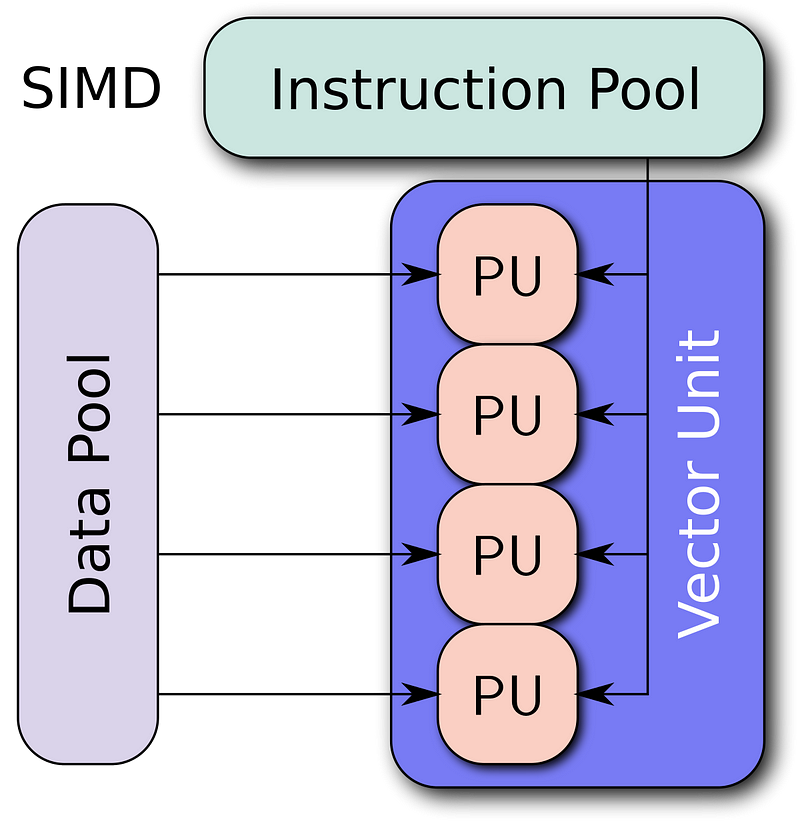
Muitas CPUs têm conjuntos de instruções “vetor” ou “SIMD” (Única instrução, vários dados) que aplicam a mesma operação simultaneamente a dois, quatro ou mais dados. O SIMD se tornou popular em CPUs de uso geral no início dos anos 90.
Para informações mais detalhadas, procure a classificação de Flynn.
Vectorização é o processo de reescrever um loop, de modo que, em vez de processar um único elemento de um array N vezes, ele processe (digamos) 4 elementos do array simultaneamente N / 4 vezes.
A Numpy implementou fortemente a vetorização em seus algoritmos. Aqui está uma nota oficial do numpy.
A vetorização descreve a ausência de qualquer looping, indexação, etc. explícitos no código - essas coisas estão ocorrendo, é claro, apenas “nos bastidores” no código C otimizado e pré-compilado. O código vetorizado possui muitas vantagens, entre as quais estão:
código vetorizado é mais conciso e mais fácil de ler
menos linhas de código geralmente significa menos bugs
o código se assemelha mais à notação matemática padrão (tornando mais fácil, normalmente, codificar corretamente construções matemáticas)
a vetorização resulta em mais código “Pythonic”. Sem vetorização, nosso código ficaria cheio de ineficientes e difíceis de ler por loops.
Exemplo de código:
## para adicionar duas matrizes juntas.
## considere duas listas básicas de python. a = [1,2,3,4,5] b = [2,3,4,5,6] c = []
## sem vetorização.
para i na faixa (len (a)): c.append (a [i] + b [i])
## usando vetorização.
a = np.array ([1,2,3,4,5]) b = np.array ([2,3,4,5,6]) c = a + b
O exemplo de código acima é um exemplo excessivamente simplificado de vetorização. E a vetorização realmente aparece quando os dados de entrada se tornam grandes.
Para mais detalhes sobre vetorização, veja aqui.
Radiodifusão:
O próximo conceito importante é a transmissão. Sir Jeremy Howard em uma de suas palestras de aprendizado de máquina, disse que a transmissão é provavelmente a ferramenta mais importante e uma habilidade para um programador de aprendizado de máquina.
The term broadcasting describes how numpy treats arrays with
different shapes during arithmetic operations. Subject to certain
constraints, the smaller array is “broadcast” across the larger
array so that they have compatible shapes. Broadcasting provides a
means of vectorizing array operations so that looping occurs in C
instead of Python. It does this without making needless copies of
data and usually leads to efficient algorithm implementations.
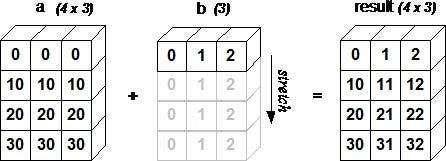
exemplo de código:
a = np.array ([1.0, 2.0, 3.0]) b = 2.0 a * b matriz ([2., 4., 6.])
isso é semelhante a
a = np.array ([1.0, 2.0, 3.0]) b = np.array ([2.0, 2.0, 2.0]) a * b matriz ([2., 4., 6.])
A matriz b é expandida para que a operação aritmética possa ser aplicada.
A radiodifusão não é um conceito novo. É uma ferramenta antiga e antiga que remonta aos anos 50. Em seu artigo “ Notação como ferramenta de pensamento ” , Kenneth Iverson descreve várias ferramentas para uso matemático que nos permitem pensar em novas perspectivas. Broadcasting foi mencionado pela primeira vez por ele não como um algoritmo de computador, mas como um procedimento matemático.Ele implementou muitas dessas ferramentas em um software chamado APL .
Seu filho mais tarde ampliou suas idéias e passou a criar outro software chamado J software . Esse gesto significa que, com o software, o que obtemos são mais de 50 anos de pesquisa profunda e o uso deles permite implementar funções matemáticas muito complexas em um pequeno trecho de código.
Também é muito útil que essas pesquisas também tenham encontrado seu caminho em idiomas que usamos hoje, como python e numpy.
Portanto, tenha em mente que essas não são idéias muito simples que vieram da noite para o dia. Estas são como as formas fundamentais de pensar em matemática e sua implementação em software. (O conteúdo acima é extraído do curso de aprendizado de máquina fast.ai).
Ok, isso é o suficiente, este artigo introduziu muitas novas palavras e terminologias para o iniciante. Mas eu também pulei vários conceitos profundos de álgebra vetorial. Isso pode ser esmagador, mas ainda assim eu tornei os conceitos tão práticos quanto possível, !)
Como comecei a aprender profundamente, decidi ajudar outras pessoas que começaram, fornecendo-lhes artigos intuitivos sobre terminologias e materiais de aprendizagem profunda. Então, se você sentir algum erro nesses artigos, por favor poste nos comentários.
Abaixo estão alguns dos recursos úteis:
Vídeos de álgebra linear intuitivos em profundidade: 3blue1brown
Melhor site para aprender aprendizagem profunda: fast.ai
Um livro de aprendizagem completo: livro de aprendizagem profunda de Ian Goodfellow.




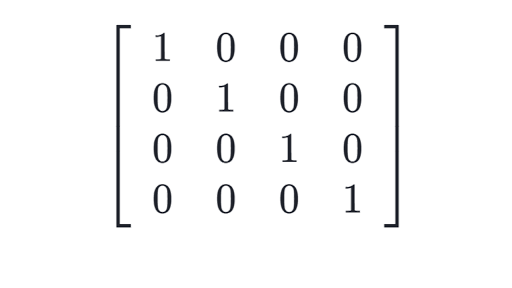
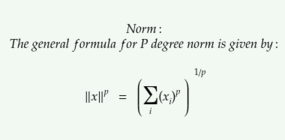
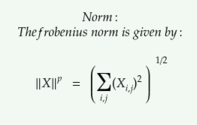


Comentários
Postar um comentário