Cinco paradoxos de machine learning que mudarão a maneira como você pensa sobre os dados

Paradoxos são uma das maravilhas da cognição humana que são difíceis de usar matemática e estatística. Conceitualmente, um paradoxo é uma afirmação que leva a uma aparente conclusão autocontraditória baseada nas premissas originais do problema. Mesmo os paradoxos mais conhecidos e bem documentados costumam enganar os especialistas do domínio, uma vez que contradizem fundamentalmente o senso comum. Como a inteligência artificial (IA) procura recriar a cognição humana, é muito comum que os modelos de aprendizado de máquina encontrem padrões paradoxais nos dados de treinamento e cheguem a conclusões que parecem contraditórias à primeira vista. Hoje, gostaria de explorar alguns dos famosos paradoxos que são comumente encontrados em modelos de aprendizado de máquina.

Paradoxos são tipicamente formulados na intersecção entre matemática e filosofia. Um notório paradoxo filosófico é conhecido como o Navio de Teseu questiona se um objeto que teve todos os seus componentes substituídos permanece fundamentalmente o mesmo objeto. Primeiro, suponha que o famoso navio navegou pelo herói Teseuem uma grande batalha foi mantida em um porto como uma peça de museu. Com o passar dos anos, algumas das peças de madeira começam a apodrecer e são substituídas por novas. Depois de um século, todas as partes foram substituídas. O navio “restaurado” ainda é o mesmo objeto que o original? Como alternativa, suponha que cada uma das peças removidas fosse armazenada em um depósito e, após o século, a tecnologia se desenvolvesse para curar seu apodrecimento e permitir que fossem reunidas para fazer um navio. Este navio “reconstruído” é o navio original? E se sim, o navio restaurado no porto ainda é o navio original?

O campo da matemática e estatística se cheio de famosos paradoxos. Para usar alguns exemplos famosos, o lendário matemático e filósofo Bertrand Russellformulou um paradoxo que destacou uma contradição em algumas das ideias mais poderosas da teoria dos conjuntos formulada como um dos maiores matemáticos de todos os tempos: Greg Cantor. Em essência, o paradoxo de Russell questiona se uma “lista de todas as listas que não se contêm”. O paradoxo surge dentro da teoria dos conjuntos nativos considerando o conjunto de todos os conjuntos que não são membros de si mesmos. Tal conjunto parece ser um membro de si se e somente se não for um membro de si mesmo. Daí o paradoxo. Alguns conjuntos, como o conjunto de todas as xícaras, não são membros de si mesmos. Outros conjuntos, como o conjunto de todos os não-xícaras, são membros de si mesmos. Chame o conjunto de todos os conjuntos que não são membros de si mesmos " R " . Se R é um membro de si mesmo, então, por definição, não deve ser um membro de si mesmo. Da mesma forma, se R não for um membro de si mesmo, então, por definição, ele deve ser um membro de si mesmo. O que????

Paradoxos famosos em modelos de aprendizado de máquina

Como qualquer forma de construção de conhecimento baseada em dados, os modelos de aprendizado de máquina não estão isentos de paradoxos cognitivos. Muito pelo contrário, à medida que o aprendizado de máquina tenta inferir padrões ocultos nos conjuntos de dados de treinamento e validar seu conhecimento em um ambiente específico, eles são constantemente vulneráveis ​​a conclusões paradoxais. Aqui estão alguns dos mais notórios paradoxos que surgem nas soluções de aprendizado de máquina.

O Paradoxo do Simpson

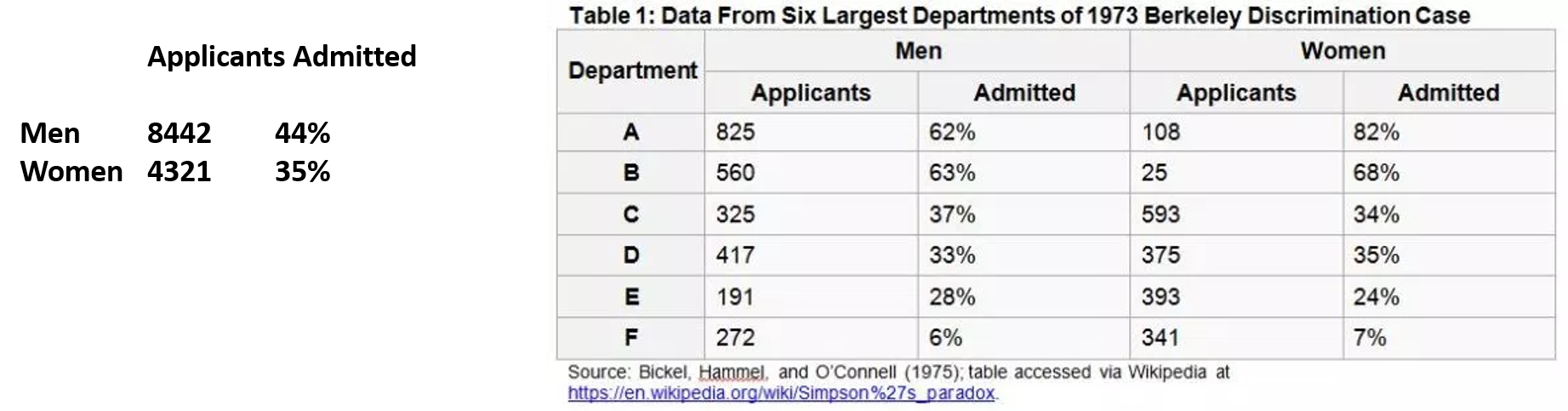
Nomeado em homenagem ao matemático britânico Edward Simpson, o Paradoxo de Simpson descreve um fenômeno em que uma tendência que é muito aparente vários grupos de dados se dissipa como os dados dentro desses grupos combinados. Um caso real do paradoxo aconteceu em 1973. As taxas de admissão foram investigadas nas escolas de pós-graduação da Universidade de Berkeley. A universidade foi processada por mulheres pelo hiato de gênero nas admissões. Os resultados da investigação foram: Quando cada escola foi analisada separadamente (direito, medicina, engenharia etc.) , as mulheres foram admitidas em uma taxa mais alta do que os homens! No entanto, a média sugeriu que os homens foram internados em uma taxa muito maior do que as mulheres. Como isso é possível?

A explicação para o caso de uso anterior é que uma média simples não leva em conta a relevância de um grupo específico no conjunto de dados geral.Neste exemplo específico, as mulheres aplicavam-se em grande número a escolas com baixas taxas de admissão: como a lei e a medicina. Essas escolas receberam menos de 10% dos estudantes. Portanto, a porcentagem de mulheres aceitas foi muito baixa. Os homens, por outro lado, tendem a aplicar-se em maior número a escolas com altas taxas de admissão: como a engenharia, onde as taxas de admissão são de cerca de 50%. Portanto, a porcentagem de homens aceitos era muito alta.

No contexto da aprendizagem de máquina, muitos algoritmos de aprendizado não supervisionados inferem padrões de conjuntos de dados de treinamento diferentes que resultam em contradições quando combinados em todos os níveis.

O Paradoxo do Braess

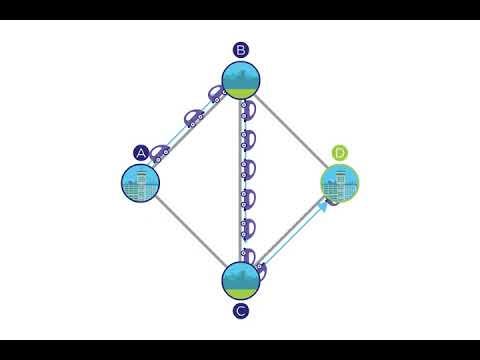
Este paradoxo foi proposto em 1968 pelo matemático alemão Dietrich Braes. Usando um exemplo de redes de tráfego congestionado, Braes explicou que, contrariando, adicionar uma estrada a uma rede de estradas poderia impedir seu fluxo (por exemplo, o tempo de viagem de cada motorista); equivalentemente, o fechamento de estradas poderia melhorar os tempos de viagem. O raciocínio de Braess baseia-se no fato de que, em um jogo de equilíbrio de Nash, os motoristas não têm incentivo para mudar suas rotas. Em termos de teoria dos jogos, um indivíduo não tem nada a ganhar com a aplicação de novas estratégias se outros se ativerem aos mesmos. Aqui, no caso dos motoristas, uma estratégia é uma rota adotada. No caso do paradoxo de Braess, os motoristas continuarão a mudar até atingirem o equilíbrio de Nash, apesar da redução no desempenho geral. Então, contraintuitivamente, fechar as estradas pode aliviar o congestionamento.

O Paradoxo de Braess é muito relevante em cenários autônomos de aprendizado de reforço com múltiplos agentes, nos quais os modelos precisam recompensar os agentes com base em decisões específicas em ambientes desconhecidos.

O paradoxo de Moravec

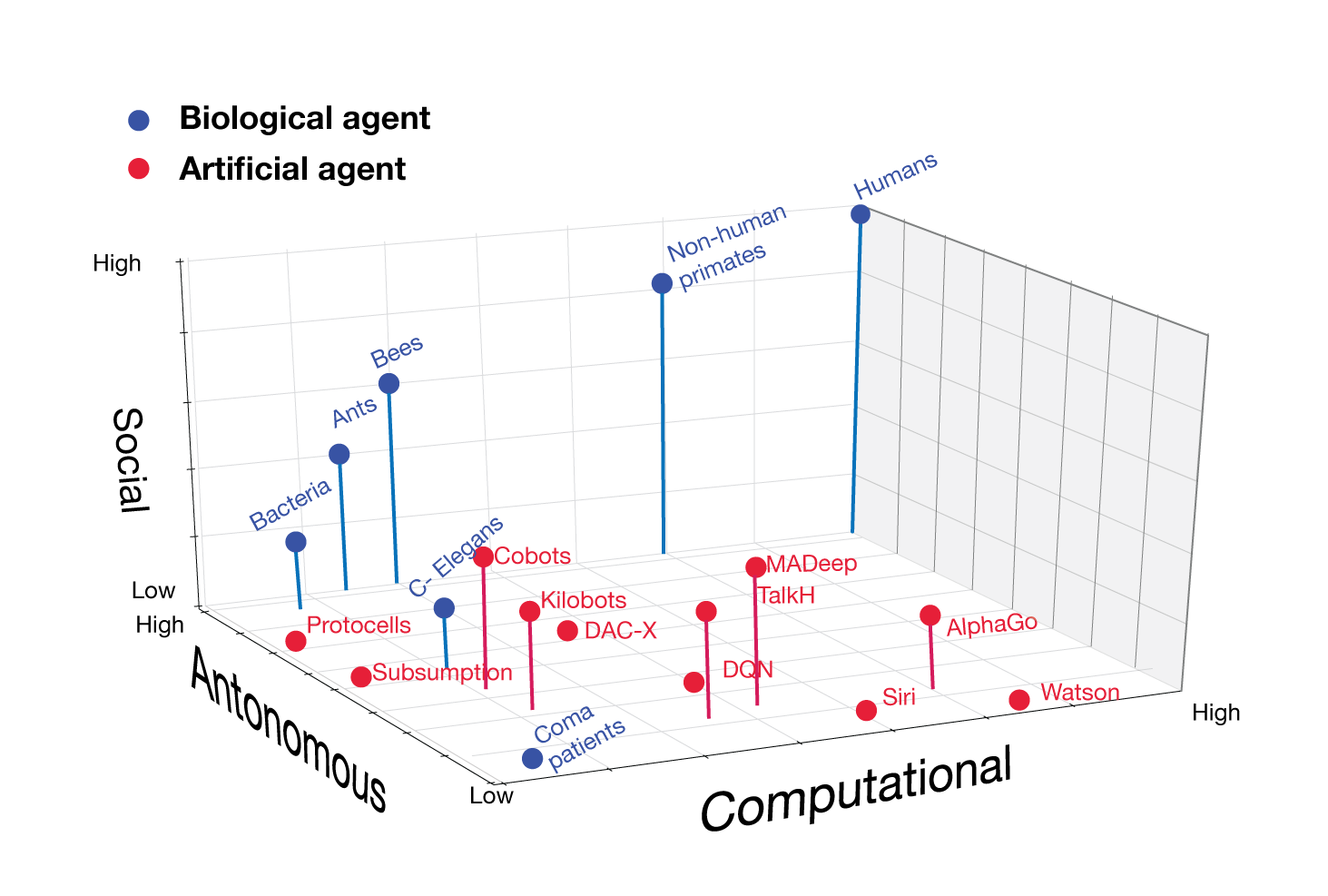
Hans Moravec pode ser considerado um dos maiores pensadores de IA das últimas décadas. Nos anos 80, a Moravec formulou uma proposição contra-intuitiva para o modo como os modelos de IA adquirem conhecimento. O Paradoxo Moravec afirma que, ao contrário do que se acredita popular, o raciocínio de alto nível requer menos computação do que a cognição inconsciente de baixo nível. Esta é uma observação empírica que vai contra a noção de que maior capacidade computacional leva a sistemas mais inteligentes.

Uma maneira mais simples de enquadrar o Paradoxo de Moravec é que os modelos de IA podem realizar tarefas incrivelmente complexas de inferência estatística e de dados que resultam impossíveis para os seres humanos. No entanto, muitas tarefas que resultam triviais para humanos, como pegar um objeto, exigem modelos caros de IA. Como escreve Moravec, “é comparativamente fácil fazer com que os computadores exibam desempenho de nível adulto em testes de inteligência ou jogar damas, e difícil ou impossível lhes dar as habilidades de um ano quando se trata de percepção e mobilidade”.

Do ponto de vista do aprendizado de máquina, o Paradoxo do Moravec é muito aplicável no aspecto da aprendizagem de transferência, que busca generalizar o conhecimento em diferentes modelos de aprendizado de máquina. Além disso, o Paradoxo de Moravec nos ensina que algumas das melhores aplicações da inteligência de máquina virão como uma combinação de humanos e algoritmos.

O paradoxo da precisão

Diretamente relacionado ao aprendizado de máquina, o Paradoxo da Precisão afirma que, contraintuitivamente, a precisão nem sempre é uma boa métrica para classificar a eficácia dos modelos preditivos. Como isso é para uma declaração confusa? O Accuracy Para tem suas raízes em conjuntos de dados de treinamento desequilibrados. Por exemplo, em um conjunto de dados em que a incidência da categoria A é dominante, sendo encontrada em 99% dos casos, a previsão de que cada caso da categoria A terá uma precisão de 99% é completamente equivocada.

Uma maneira mais simples de entender o Paradoxo de Precisão é encontrar o equilíbrio entre precisão e recordação em modelos de aprendizado de máquina. Nos algoritmos de aprendizado de máquina, a precisão é geralmente definida como a medida de qual fração de suas previsões para a classe positiva é válida. É formulado por (True Positives / True Positives + False Positivo). Complementarmente, a métrica de recordação mede a frequência com que suas previsões realmente capturam a classe positiva. É formulado por (True Positives / True Positives + False Negatives).

Em muitos modelos de aprendizado de máquina, o equilíbrio entre precisão e recuperação resulta em uma melhor métrica de precisão. Por exemplo, no caso de um algoritmo para a detecção de fraudes, a rechamada é uma métrica mais importante. Obviamente, é importante capturar todas as fraudes possíveis, mesmo que isso signifique que as autoridades precisem passar por alguns falsos positivos. Por outro lado, se o algoritmo é criado para análise de sentimento e tudo o que você precisa é uma ideia de alto nível de emoções indicada nos tweets, então, buscar precisão é o caminho a percorrer.

O paradoxo da Learnability-Godel

Salvando o mais controverso para o final, este é um paradoxo muito recente que foi publicado em um trabalho de pesquisa no início deste ano . O paradoxo liga a capacidade de um modelo de aprendizado de máquina de aprender a uma das teorias mais controversas da matemática: o Teorema da Incompletude de Gödel .

Kurt Gödel é um dos mais brilhantes matemáticos de todos os tempos e um dos que ultrapassou os limites da filosofia, da física e da matemática, como alguns de seus predecessores. Em 1931, Gödel publicou seus dois teoremas da incompletude que essencialmente dizem que algumas afirmações não podem ser provadas verdadeiras ou falsas usando linguagem matemática padrão. Em outras palavras, a matemática é uma linguagem insuficiente para entender alguns aspectos do universo. Os teoremas vieram a ser conhecidos como a hipótese do continuum de Gödel.

Em um trabalho recente, pesquisadores de IA do Instituto de Tecnologia de Israel ligaram a hipótese do continuum de Gödel à capacidade de aprendizado de um modelo de aprendizado de máquina. Em uma afirmação paradoxal que desafia toda a sabedoria comum, os pesquisadores definem a noção de um limbo de aprendizado. Essencialmente, os pesquisadores mostram que, se a hipótese do continuum é verdadeira, uma pequena amostra é suficiente para fazer a extrapolação. Mas se for falso, nenhuma amostra finita pode ser suficiente. Dessa forma, eles mostram que o problema da capacidade de aprender é equivalente à hipótese do contínuo. Portanto, o problema da capacidade de aprendizado também está em um estado de limbo que só pode ser resolvido escolhendo o universo axiomático.

Em termos simples, as provas matemáticas do estudo mostram que os problemas de IA estão sujeitos à hipótese do continuum de Gödel, o que significa que muitos problemas podem ser efetivamente insolúveis pela IA. Embora esse paradoxo tenha pouquíssimas aplicações para os problemas da IA ​​do mundo real hoje, será fundamental para a evolução do campo no futuro próximo.

Paradoxos são onipresentes em problemas de aprendizado de máquina no mundo real. Você pode argumentar que, como os algoritmos não têm uma noção de bom senso, eles podem estar imunes a paradoxos estatísticos. No entanto, dado que a maioria dos problemas de aprendizado de máquina requer análise e intervenções humanas e é baseada em conjuntos de dados com curadoria humana, nós vamos viver em um universo de paradoxos por algum tempo.