Obtendo o básico de correlação e covariância
A correlação é um dos conceitos estatísticos amplamente utilizados. Esta postagem do blog tenta responder o que é correlação, por que é tão útil, que correlação de relacionamento e covariância compartilham e algumas maneiras de calcular a correlação.

O que é correlação?
Correlação, técnica estatística que determina como uma variável se move / muda em relação à outra variável. Isso nos dá a idéia sobre o grau de relacionamento das duas variáveis. É uma medida de análise bi-variável que descreve a associação entre diferentes variáveis. Na maioria dos negócios, é útil expressar um assunto em termos de relacionamento com outros.
Por exemplo: as vendas podem aumentar se muito dinheiro for gasto em marketing de produtos.
Por que é útil?
1. Se duas variáveis estão intimamente correlacionadas, podemos prever uma variável da outra.
2. A correlação desempenha um papel vital na localização de variáveis importantes das quais outras variáveis dependem.
3. É usado como base para várias técnicas de modelagem.
4. A análise de correlação adequada leva a uma melhor compreensão dos dados.
5. A correlação contribui para a compreensão do relacionamento causal (se houver).
Relação de Correlação e Covariância
Antes de mergulhar mais na correlação, vamos entender a covariância.
Covariância : O prefixo 'Co' define algum tipo de ação conjunta e a variação refere-se à mudança ou variação. Por isso, duas variáveis são relacionadas com base em como essas variáveis mudam em relação uma à outra.
Mas espere, a covariância é igual à correlação?
Como a covariância diz algo na mesma linha que a correlação, a correlação dá um passo além da covariância e também nos fala sobre a força do relacionamento.
Ambos podem ser positivos ou negativos. A covariância é positiva se um aumenta outro também aumenta e negativa se um aumenta outro diminui.
A covariância é calculada como

Xᵢ = ponto de observação da variável X
x̅ = Média de todas as observações (X)
Yᵢ = ponto de observação da variável Y
ȳ = Média de todas as observações (Y)
n = Número de observações
Decodificando a fórmula de covariância: Covariância entre duas variáveis x e y é a soma dos produtos das diferenças de cada item e suas respectivas médias divididas pelo número de itens no conjunto de dados menos um.
Para entender melhor com um exemplo simples de dados de amostra:
Os dados a seguir mostram o número de clientes com a temperatura correspondente.

Primeiro encontre as médias de ambas as variáveis, subtraia cada item com sua respectiva média e multiplique-as da seguinte forma
Média de X, x̅ = (97 + 86 + 89 + 84 + 94 + 74) / 6 = 524/6 = 87,333
Média de Y, Ȳ = (14 + 11 + 9 + 9 + 15 + 7) / 6 = 65/6 = 10,833

COV ( x, y ) = 112,33 / (6–1) = 112,33 / 5 = 22,46
A covariância entre a temperatura e os clientes é 22,46. Como a covariância é positiva, a temperatura e o número de clientes têm um relacionamento positivo. À medida que a temperatura aumenta, o número de clientes também aumenta.
Mas aqui não há informações sobre quão forte é o relacionamento, e é aí que a correlação entra em cena.
Coeficiente de correlação é o termo usado para referir o resultado de qualquer método de medição de correlação.
Portanto, aqui, o coeficiente de correlação da amostra é calculado como

COV ( x, y ) = covariância das variáveis x e y
σ x = desvio padrão da amostra da variável x
σ y = desvio padrão da amostra da variável y
σ x = desvio padrão da amostra da variável x
σ y = desvio padrão da amostra da variável y

COV (x, y) = 22,46
σx = 331,28 / 5 = 66,25 = 8,13
σy = 48,78 / 5 = 9,75 = 3,1
correlação = 22,46 / (8,13x 3,1) = 22,46 / 25,20 = 0,8
0.8 mostra que a força da correlação entre temperatura e número de clientes é muito forte.
O coeficiente de correlação da amostra pode ser usado para estimar o coeficiente de correlação da população.
Existem métodos diferentes para calcular o coeficiente de correlação entre dois sujeitos. Alguns dos métodos são:
1. Coeficiente de correlação de Pearson
Ele captura a força e a direção da associação linear entre duas variáveis contínuas. Ele tenta traçar a linha de melhor ajuste através dos pontos de dados de duas variáveis. O coeficiente de correlação de Pearson indica a que distância esses pontos de dados estão da linha de melhor ajuste. O relacionamento é linear somente quando a mudança em uma variável é proporcional à mudança em outra variável.

Coeficiente de correlação de Pearson calculado como

r = Coeficiente de correlação de Pearson
n = número de observações
∑xy = soma dos produtos dos valores de xey
∑x = soma dos valores de xyy = soma dos valores
de y
∑x2 = soma dos valores de x ao quadrado
∑y2 = soma dos valores de y ao quadrado
∑xy = soma dos produtos dos valores de xey
∑x = soma dos valores de xyy = soma dos valores
de y
∑x2 = soma dos valores de x ao quadrado
∑y2 = soma dos valores de y ao quadrado
Coeficiente de Correlação de Spearman
Ele tenta determinar a força e a direção do relacionamento monotônico que existe entre duas variáveis ordinais ou contínuas. Em um relacionamento monotônico, duas variáveis tendem a mudar juntas, mas não com a taxa constante. É calculado com base nos valores classificados das variáveis, e não nos dados brutos.
As relações monotônicas e não monotônicas são mostradas abaixo:


ρ = coeficiente de correlação de Spearman rank
di = a diferença entre as fileiras das variáveis correspondentes
n = número de observações
di = a diferença entre as fileiras das variáveis correspondentes
n = número de observações
Comparação: coeficiente de correlação de Pearson e Spearman
O coeficiente de correlação de Pearson e Spearman pode levar valores de -1 a 1.
(i) Se uma variável aumenta com a outra variável na taxa consistente, o coeficiente de Pearson seria 1, o que resulta em uma linha perfeita. Nesse caso, o coeficiente de Spearman também seria 1.

(ii) Se uma variável aumenta com a outra variável, mas não com a taxa consistente, o coeficiente de Pearson seria positivo, mas menor que 1. Nesse caso, o coeficiente de Spearman ainda seria 1.

(iii) Se o relacionamento for aleatório, ambos os coeficientes seriam próximos de 0.
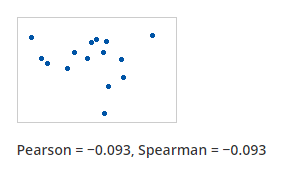
(iv) Se a relação entre as variáveis for uma linha perfeita, mas com uma relação decrescente, os dois coeficientes serão -1.

(v) Se a relação entre duas variáveis for tal que uma variável diminua quando a outra aumentar, mas não com a taxa consistente, o coeficiente de Pearson seria negativo, mas maior que -1. O coeficiente de Spearman seria -1 neste caso.
Quando usar o que?
A correlação de Pearson descreve relações lineares e a correlação de spearman descreve relações monotônicas. Um gráfico de dispersão seria útil para visualizar os dados e entender qual coeficiente de correlação deve ser usado. Outra maneira de fazer é aplicar os métodos e verificar se o desempenho está bom. Por exemplo, se os resultados mostram que o coeficiente de correlação de lança é maior que o coeficiente de Pearson, isso significa que nossos dados têm relações monotônicas e não lineares.
Mais Lê:
Obrigado pela leitura!

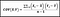






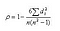







Comentários
Postar um comentário