Como escolher a melhor métrica de avaliação para problemas de classificação
Um guia abrangente que cobre as métricas de avaliação mais comumente usadas para classificação supervisionada e sua utilidade em diferentes cenários
Para avaliar adequadamente um modelo de classificação, é importante considerar cuidadosamente qual métrica de avaliação é a mais adequada.
Este artigo abordará as métricas de avaliação mais comumente usadas para tarefas de classificação, incluindo casos de exemplo relevantes, e fornecerá as informações necessárias para ajudá-lo a escolher entre elas.
Classificação
Um problema de classificação é caracterizado pela previsão da categoria ou classe de uma determinada observação com base em suas características correspondentes. A escolha da métrica de avaliação mais adequada dependerá dos aspectos de desempenho do modelo que o usuário deseja otimizar.
Imagine um modelo de predição com o objetivo de diagnosticar uma determinada doença. Se esse modelo não detectar a doença, pode levar a consequências graves, como atraso no tratamento e danos ao paciente. Por outro lado, se o modelo diagnosticar falsamente um paciente saudável, isso também pode resultar em consequências dispendiosas ao submeter um paciente saudável a testes e tratamentos desnecessários.
Em última análise, a decisão sobre qual erro minimizar dependerá do caso de uso específico e dos custos associados a ele. Vamos examinar algumas das métricas mais usadas para esclarecer um pouco mais sobre isso.
Métricas de avaliação
Precisão
Quando as classes em um conjunto de dados são balanceadas, ou seja, se houver aproximadamente um número igual de amostras em cada classe, a precisão pode servir como uma métrica simples e intuitiva para avaliar o desempenho de um modelo.
Em termos simples, a precisão mede a proporção de previsões corretas feitas pelo modelo.
Para ilustrar isso, vamos dar uma olhada na tabela a seguir, mostrando as classes reais e previstas:
Neste exemplo, temos um total de 10 amostras, das quais 6 foram previstas corretamente (sombreamento verde).
Assim, nossa precisão pode ser calculada da seguinte forma:
Para nos prepararmos para o que está por vir com as métricas abaixo, vale ressaltar que as previsões corretas são a soma de verdadeiros positivos e verdadeiros negativos .
Um verdadeiro positivo (TP) ocorre quando o modelo prevê corretamente a classe positiva.
Um verdadeiro negativo (TN) ocorre quando o modelo prevê corretamente a classe negativa.
Em nosso exemplo, um verdadeiro positivo é um resultado em que as classes real e prevista são 1.
Exemplo: Detecção facial. Para detectar a ausência ou a presença de um rosto em uma imagem, a precisão pode ser uma métrica adequada, pois o custo de um falso positivo (identificar um não-rosto como um rosto) ou um falso negativo (não identificar um rosto) é Aproximadamente igual. Observação: a distribuição dos rótulos de classe no conjunto de dados deve ser balanceada para que a precisão seja uma medida apropriada.
Precisão
A métrica de precisão é adequada para medir a proporção de previsões positivas corretas.
Em outras palavras, a precisão fornece uma medida da capacidade do modelo de identificar corretamente amostras positivas verdadeiras.
Como resultado, é frequentemente usado quando o objetivo é minimizar falsos positivos, como é o caso em domínios como detecção de fraude de cartão de crédito ou diagnóstico de doenças.
Um falso positivo (PF) ocorre quando o modelo prevê incorretamente a classe positiva, indicando que uma determinada condição existe quando na realidade não existe.
Em nosso exemplo, um falso positivo é um resultado em que a classe prevista deveria ser 0, mas na verdade era 1.
Exemplo: Detecção de anomalias. Na detecção de fraudes, por exemplo, a precisão pode ser uma métrica de avaliação adequada, principalmente quando o custo de falsos positivos é alto. Identificar atividades não fraudulentas como fraudulentas pode levar não apenas a custos adicionais para despesas de investigação, mas também a altos níveis de insatisfação do cliente e aumento das taxas de rotatividade.
Lembrar
Quando o objetivo de uma tarefa de previsão é minimizar falsos negativos, o recall serve como uma métrica de avaliação apropriada.
Recall mede a proporção de verdadeiros positivos que são identificados corretamente pelo modelo.
É particularmente útil em situações em que os falsos negativos são mais caros do que os falsos positivos.
Um falso negativo (FN) ocorre quando o modelo prevê incorretamente a classe negativa, indicando que uma determinada condição está ausente quando de fato está presente.
Em nosso exemplo, um falso negativo é um resultado em que a classe prevista deveria ser 1, mas na verdade era 0.
Exemplo: Diagnóstico de doença. Nos testes de COVID-19, por exemplo, o recall é uma boa escolha quando o objetivo é detectar o maior número possível de casos positivos. Nesse caso, um número maior de falsos positivos é tolerado, pois a prioridade é minimizar os falsos negativos para evitar a propagação da doença. Indiscutivelmente, o custo de perder um caso positivo é muito maior do que classificar erroneamente um caso negativo como positivo.
Pontuação F1
Nos casos em que falsos positivos e falsos negativos são aspectos importantes a serem considerados, como na detecção de spam, a pontuação F1 é uma métrica útil.
A pontuação F1 é a média harmônica de precisão e recuperação e fornece uma medida equilibrada do desempenho do modelo, levando em consideração falsos positivos e falsos negativos.
É calculado da seguinte forma:
Exemplo: classificação de documentos. Na detecção de spam, por exemplo, a pontuação F1 é uma métrica de avaliação apropriada, pois o objetivo é encontrar um equilíbrio entre precisão e revocação. Um classificador de e-mail de spam deve classificar corretamente o maior número possível de e-mails de spam (recall), além de evitar a classificação incorreta de e-mails legítimos como spam (precisão).
Área sob a curva ROC (AUC)
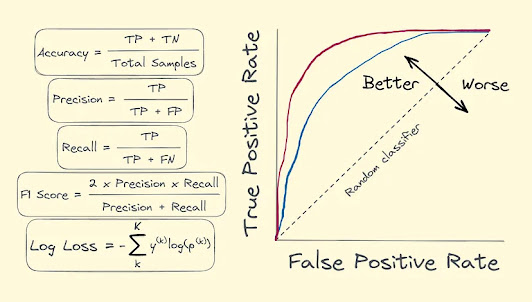
A curva característica de operação do receptor, ou curva ROC , é um gráfico que ilustra o desempenho de um classificador binário em todos os limites de classificação.
A área sob a curva ROC, ou AUC , mede o quão bem um classificador binário pode diferenciar classes positivas e negativas em diferentes limiares.
É uma métrica particularmente útil quando o custo de falsos positivos e falsos negativos é diferente. Isso ocorre porque ele considera a compensação entre a taxa de verdadeiros positivos (sensibilidade) e a taxa de falsos positivos (especificidade 1) em diferentes limiares. Ao ajustar o limite, podemos obter um classificador que prioriza a sensibilidade ou a especificidade, dependendo do custo de falsos positivos e falsos negativos de um problema específico.
A taxa de verdadeiro positivo (TPR) , ou sensibilidade , mede a proporção de casos positivos reais que são identificados corretamente pelo modelo. É exatamente o mesmo que recordar.
É calculado da seguinte forma:
A taxa de falso positivo (FPR) , ou 1-especificidade , mede a proporção de casos negativos reais que são incorretamente classificados como positivos pelo modelo.
É calculado da seguinte forma:
Quanto mais próxima a curva ROC estiver do canto superior esquerdo, melhor será o desempenho do classificador. Uma AUC correspondente de 1 indica classificação perfeita, enquanto uma AUC de 0,5 indica desempenho de classificação aleatória.
Exemplo: problemas de classificação. Quando a tarefa é classificar amostras por sua probabilidade de pertencer a uma classe ou outra, a AUC é uma métrica adequada, pois reflete a capacidade do modelo de classificar amostras corretamente, em vez de apenas classificá-las. Por exemplo, ele pode ser usado em publicidade on-line, pois avaliaria a capacidade do modelo de classificar corretamente os usuários por sua probabilidade de clicar em um anúncio, em vez de apenas prever um resultado binário de clique/não-clique.
Perda de registro
A perda logarítmica, também conhecida como perda de log ou perda de entropia cruzada, é uma métrica de avaliação útil para problemas de classificação em que estimativas probabilísticas são importantes.
A perda de log mede a diferença entre as probabilidades previstas das classes e os rótulos de classe reais.
É uma métrica particularmente útil quando o objetivo é penalizar o modelo por ser excessivamente confiante em prever a classe errada. A métrica também é usada como função de perda no treinamento de regressores logísticos e redes neurais.
Para uma única amostra, em que y denota o rótulo verdadeiro e p denota a estimativa de probabilidade, a perda de log é calculada da seguinte forma:
Quando o rótulo verdadeiro é 1, a perda de log em função das probabilidades previstas se parece com isto:
Pode-se ver claramente que a perda de log fica menor quanto mais certo o classificador está sobre o rótulo correto ser 1.
A perda de log também pode ser generalizada para problemas de classificação multiclasse. Para uma única amostra, onde k denota o rótulo da classe e K corresponde ao número total de classes, pode ser calculado da seguinte forma:
Na classificação binária e multiclasse, a perda de log é uma medida útil que determina o quão bem as probabilidades previstas correspondem aos verdadeiros rótulos de classe.
Exemplo: Avaliação de risco de crédito. Por exemplo, a perda de log pode ser usada para avaliar o desempenho de um modelo de risco de crédito que prevê a probabilidade de um mutuário inadimplir um empréstimo. O custo de um falso negativo (prever um mutuário confiável como não confiável) pode ser muito maior do que o de um falso positivo (prever um mutuário não confiável como confiável). Assim, minimizar a perda de log pode ajudar a minimizar o risco financeiro do empréstimo nesse cenário.
Conclusão
Para avaliar com precisão o desempenho de um classificador e tomar decisões informadas com base em suas previsões, é crucial escolher uma métrica de avaliação apropriada. Na maioria das situações, essa escolha dependerá muito do problema específico em questão. Fatores importantes a serem considerados são o equilíbrio das classes em um conjunto de dados, se é mais importante minimizar falsos positivos, falsos negativos ou ambos, e a importância da classificação e das estimativas probabilísticas.


















Comentários
Postar um comentário